这篇文章简单地总结一下信息熵。
概率和编码长度
首先假设我们有离散型随机变量 X,X 总共有n个取值,每种取值的概率为p(x)。
假如X有4种可能的取值,每种取值的概率都相同,那么我们需要用2个二进制位来编码每种可能的取值。相应的,如果X有16个取值,那么需要用4个二进制位来编码。
但是如果每种取值发生的概率并不是相同的呢?例如,其中某个取值出现的概率明显要高于其他取值,如果这时候还是用相同的编码长度来编码每种可能的取值,就会造成一种浪费。一个直觉的方法是将概率大的取值分配较短的编码,概率小的取值分配稍微长的编码长度,这样使得整体的编码长度达到最短。
香农提出公式:如果概率为p(x),那么所需要的编码长度为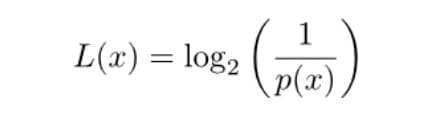
那么对于整个概率分布,平均编码长度(每种概率对应的编码长度加权求和)为
上面的公式就是信息熵 。
信息熵的含义
从上面的讨论中我们知道了:信息熵其实就等于平均编码长度。
如果熵越大,那么平均编码长度越大,能表示的可能性就越多,不确定性就越大,信息量就越大。(想想,如果平均编码长度为1,那么只能表示两种可能,这时候所能包含的信息就很少。)
对应到随机变量的概率分布上,如果概率分布越分散(极端情况下,均匀分布),那么表明这个随机变量的不确定性越高,平均编码长度越长,信息熵越大,包含的信息量越大。
同物理学中的熵做类比:物理学中,熵越大,表明越无序,对应到信息学中,表明可能性越多,包含的信息量越多。
what to take away
- 信息熵等于平均编码长度
- 信息熵越大,包含的信息量越大
- 均匀分布概率最分散,不确定性最大,信息熵最大。
参考
信息熵、交叉熵、相对熵(KL散度)
下面来叙述这3种常用熵的概念以及他们之间的联系。
从上面的讨论中我们知道:信息熵(也称为香农熵)对应着一种最优的编码方式,即找不到更短的平均编码长度了。
信息熵的公式实际上是在求1/log(p(x))的数学期望。
假如p(x)对应真实的概率分布,但在实际应用场景中,我们往往不知道真实分布,我们只能得到一个估计的概率分布q(x),这时候,我们用q(x)来编码p(x),即将原来每个p(x)对应的编码长度1/log(p(x))替换成1/log(q(x)),然后我们再计算这种编码方式对应的平均编码长度:

这就是交叉熵公式。
重点:当使用q(x)去编码p(x)时,得到的平均编码长度只会大于等于p(x)的香农熵(p(x)的最短编码长度)。等号成立的条件是q(x)完全等于p(x),如果q(x)和p(x)之间的差别越大,那么得到的编码长度差别也就越大。
从上面的讨论可以知道,使用q(x)编码p(x),得到的编码长度总是会比最短的编码长度大,那么多出来的这部分,我们定义为相对熵,也就是KL散度。
这里换一种公式来表达信息熵、交叉熵和KL散度……(因为hexo中不支持latex,我只能自己到处找别人写的公式….)
香农熵

交叉熵
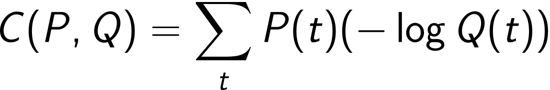
- 相对熵
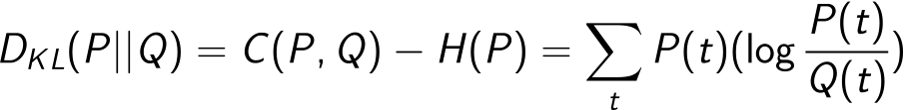
用一张图来表示这3者之间的关系如下:
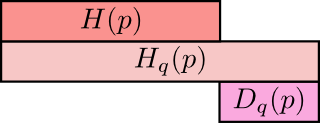
上图中,第一行表示香农熵,第二行表示交叉熵,第三行表示KL散度。所谓的KL散度,其实就是交叉熵和香农熵之间的差值,并且永远取非负值。
当交叉熵和香农熵完全相同时(即估计得到的q(x)完全等于p(x)),这时计算得到的相对熵为0.
相对熵有下面几条性质:
- 如果两个函数f(x)和g(x)完全相同,那么计算两者之间的KL散度为0。两个函数之间的差异越大,那么KL散度越大。(这里f(x)和g(x)分别对应p(x)和q(x))
- 相对熵可以用来度量两个概率分部之间的相似度,如果相对熵越小,那么说明两个概率分布越接近。
- 相对熵公式不对称,不具备交换律。即D(p, q)≠D(q, p)。

